这事儿其实是个小事儿,我断断续续搞了竟然蛮久。寻思着记录一下,不见得有多少技术含量,权当一篇流水账。
我是路标
#0. 背景
一位朋友找到我,提了一个请求。
有一个历史项目是用来解析特定的曲线文件的,已经找不到以前的人了,目前我也无法启动。翻看代码发现主要核心它引用了一个dll ,我自己用这个dll 一直提示注册失败,用以前下载你写的反编译工具也没有解析成功,想让你给看看,能不能解析,或者给看看注册失败的原因是啥,网上找的各种注册都没有成功
他所说的要注册的文件呢,是这个。
这个DLL的文件名一看就知道是一个互操作导入文件,并不是功能主体。后来他有提供给我整个项目包,大概七百多M,可是我在里面翻了翻,好像找不到这个互操作程序集对应的原程序集。而这个项目过于久远,当时这个工具集是不是买的也不清楚,这个WisToXXX方法什么个逻辑也不知道。
两天后他又找到我,说找不到之前的文件,根据以前的代码修改出来一个例子,但是速度特别慢,就问我是不是能优化。
这个包还挺大,两百多M,主要是里面包含了一个测试的数据文件,这一个文件就四百多M,而最终实现的功能,是类似于如下的这样一个计算工具。
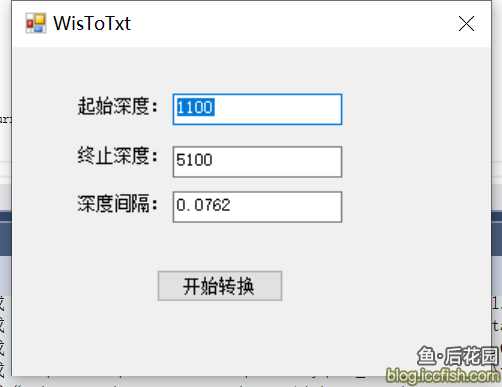
简单来说就是从起始到终止深度,以深度间隔为差值,从指定的wis数据文件中查找指定的数据,最终输出到对应的数据文件中。
他说,
想着直接调用现成的方法,没有找到。旧的代码里面以前开发有自己尝试写过,就是导出数据有问题,我改了改,导出的数据正确了,就是速度太慢。
开始的时候我没看代码,直接建议他打个时间戳看看哪里慢的,因为这数据文件也蛮大的感觉有没有可能读取时间也比较久。

从上图可以看到,当时是一个半月以前……我这效率哈哈哈哈哈,笑死。
当时我简单看了看给的项目代码(后面说),看得有点迷糊(可能是饿的),就问他说,有没有原始的算法说明。
然后他提供了一点。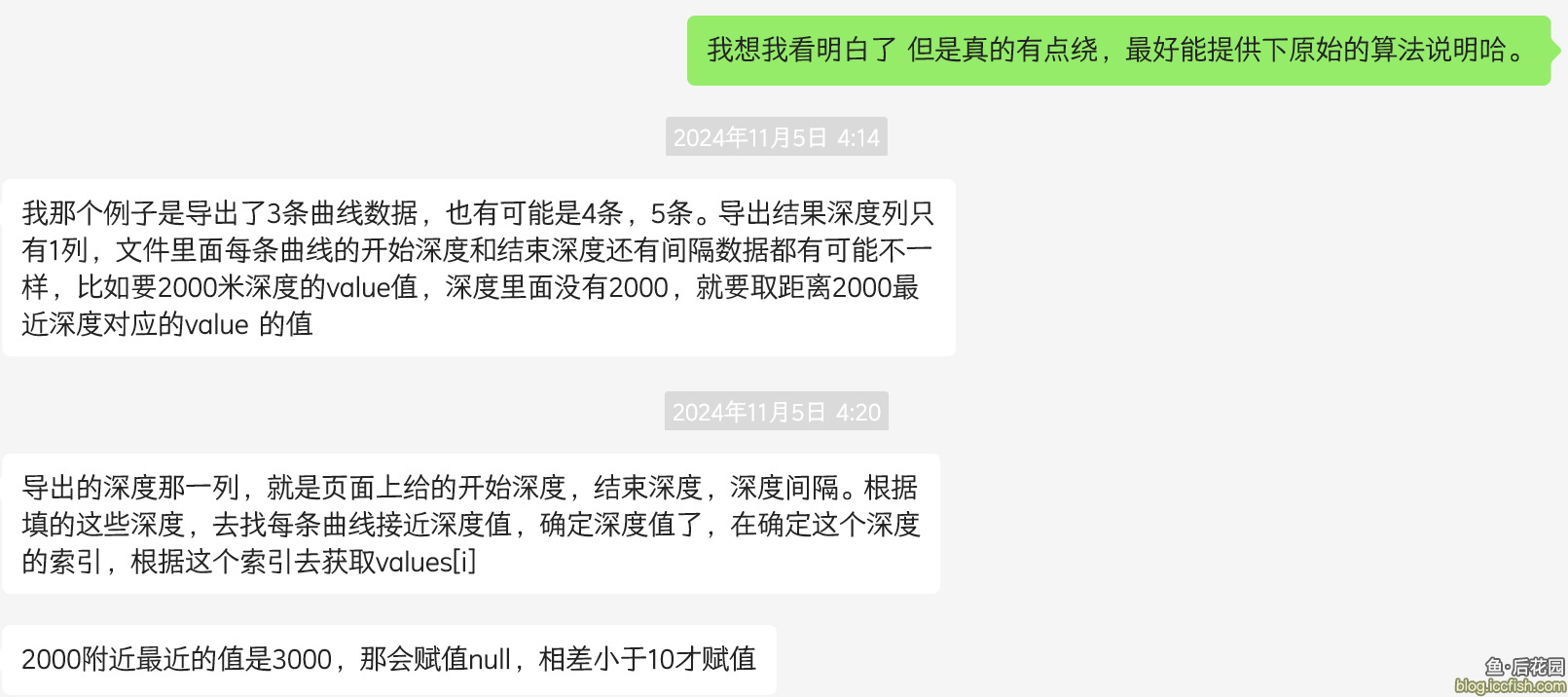
然后这事儿就给我搁置了……很久,搁置的原因不一而足,反正很多原因,我觉得吧,人生还是很……辛苦的,期间认真反思了到底什么叫岁月静好。
一转眼到11月底,兄弟憋了好久后跑来问我有没有搞,我满怀愧疚地说没有,后面抽时间看。
然后我这满怀愧疚地又继续放了两周多。
#1. 准备工作
原项目比较大(主要是wis数据文件四百多M),我就不放了。新建一个测试项目,把框架贴一贴,先搭出来一个测试的框架。
这里用Rider新建一个 .Net 4.5的控制台项目,新建一个入口文件。
public static void Main(string[] args)
{
var st = new Stopwatch();
var wisFile = "test.wis";
Console.WriteLine("Loading data...");
st.Start();
var wd = new WisDAL();
var wm = new WIS_MODEL();
var curveNameStr = new[] { "CAL1", "GR", "M2SBL" };
var start = "50.0000";
var end = "4012.0190";
var step = "0.0762";
var file = DateTime.Now.ToString("yyyyMMddHHmmss") + "_{0}.txt";
wd.Read(wm, wisFile, curveNameStr);
st.Stop();
Console.WriteLine($"Wis data loaded in {st.ElapsedMilliseconds} ms.");
void InitPrams(ICalculator calculator, string outFile)
{
calculator.WisModel = wm;
calculator.CurveNames = curveNameStr;
calculator.StartDepth = start;
calculator.EndDepth = end;
calculator.StepDepth = step;
calculator.TargetFile = outFile;
calculator.Verbose = false;
}
var c1 = new Calculator1();
Console.WriteLine("Running calculator 1...");
InitPrams(c1, string.Format(file, "c1"));
st.Start();
c1.Calculate();
st.Stop();
Console.WriteLine($"Wis calculator 1 in {st.ElapsedMilliseconds} ms.");
}这段代码做了什么事儿呢,就是从wis文件中加载了指定数据,然后创建对应的计算工作类,进行初始化后,计算数据并进行输出。
值得一提的是这里的数据加载并没有我想象的花时间,四百多M的文件,在我的机器上(配置后面说)竟然只用了10毫秒就完成了加载。
为了便于复用,新建一个抽象接口表示计算类的接口。
public interface ICalculator
{
string[] CurveNames { get; set; }
WIS_MODEL WisModel { get; set; }
string StartDepth { get; set; }
string EndDepth { get; set; }
string StepDepth { get; set; }
string TargetFile { get; set; }
/// <summary>
/// 计算
/// </summary>
void Calculate();
}
后续的接口类都基于此接口进行。
由于一部分操作是通用的,于是再新建个抽象的计算类,用于提供通用的方法。
abstract class AbstractCalculator : ICalculator
{
private Dictionary<int, string> _paddingStrMap = new Dictionary<int, string>();
public string StartDepth { get; set; }
public string EndDepth { get; set; }
public string StepDepth { get; set; }
public string[] CurveNames { get; set; }
public WIS_MODEL WisModel { get; set; }
public string TargetFile { get; set; }
public abstract void Calculate();
/// <summary>
/// 查找指定名称的数据通道
/// </summary>
/// <param name="wm"></param>
/// <param name="name"></param>
/// <returns></returns>
public WIS_CHANNLE FindChannel(WIS_MODEL wm, string name) => wm.WisCurveList.FirstOrDefault(w => w.Name == name && w.NumOfDimension == 1);
}
上面的几个函数会在后面用到。
#2. 测试平台
后续性能的基准测试基于我的笔记本,配置如下:
- CPU: Intel I9-13900HX
- 内存:DDR5 5600 64GB
- 固态硬盘:致态 TiPlus 7100 1TB
- 测试数据集:test.wis,474MB,每个曲线 50935 个点
#3. 原始写法
原始写法如下。
class Calculator1 : AbstractCalculator
{
/// <inheritdoc />
public override void Calculate()
{
var st = new Stopwatch();
try
{
st.Start();
DataTable dt = CreateDt(CurveNames); //创建导出数据
float sTDEP = StartDepth.ToSingle();
float eNDEP = EndDepth.ToSingle();
float rLEV = StepDepth.ToSingle(); //维的采集或计算增量(#DEPTH的下一个减去上一个的值)
List<WIS_CHANNLE> _WisChannleList = WisModel.WisCurveList; //WIS曲线对象集合
string cURVENAME = string.Join(", ", CurveNames); //曲线名称串
int rowIndex = 0; //初始化行索引
bool end = false;
foreach (WIS_CHANNLE _wc in _WisChannleList)
{
rowIndex = 0; //初始化行索引
//NumOfDimension对象维信息数
if (_wc.NumOfDimension == 1)
{
List<float> Depths = _wc.Depths; //深度值列表
float o = 0f; //初始值
float depth = 0f;
for (int i = 0; i <= Depths.Count + 1; i++)
{
if (i == 0)
{
o = sTDEP;
}
else
{
o = o + rLEV; //深度:下一个值=上一个的值+采样间隔
}
depth = Depths.Aggregate((current, next) => Math.Abs((long)current - o) < Math.Abs((long)next - o) ? current : next);
i = Depths.IndexOf(depth);
//深度及数据值处理
if (o >= sTDEP && o <= eNDEP)
{
DataRow dr;
if (end)
{
if (Math.Abs(depth - o) > 10)
{
dr = dt.Rows[rowIndex]; //第I行赋值
dr["#DEPTH"] = o.ToString("f4"); //深度值--f4小数保留位数
dr[_wc.Name] = null; //曲线值
rowIndex++;
}
else
{
dr = dt.Rows[rowIndex]; //第I行赋值
dr["#DEPTH"] = o.ToString("f4"); //深度值--f4小数保留位数
dr[_wc.Name] = _wc.Values[i].ToString("f4"); //曲线值
rowIndex++;
}
}
else
{
dr = dt.NewRow();
if (Math.Abs(depth - o) > 10)
{
dr["#DEPTH"] = o.ToString("f4"); //深度值--f4小数保留位数
dr[_wc.Name] = null; //曲线值
dt.Rows.Add(dr);
}
else
{
dr["#DEPTH"] = o.ToString("f4"); //深度值--f4小数保留位数
dr[_wc.Name] = _wc.Values[i].ToString("f4"); //曲线值
dt.Rows.Add(dr);
}
}
}
else
{
end = true;
break;
}
}
}
else if (_wc.NumOfDimension == 2)
{
}
}
dt.AcceptChanges(); //提交数据更改操作
st.Stop();
Console.WriteLine($"数据计算完成,耗时 {st.ElapsedMilliseconds}毫秒");
if (dt != null && dt.Rows.Count > 0)
{
st.Restart();
WriteTxt(TargetFile, cURVENAME, sTDEP.ToString("f4"), eNDEP.ToString("f4"), rLEV.ToString("f4"), dt);
st.Stop();
Console.WriteLine($"数据写入完成,耗时 {st.ElapsedMilliseconds}毫秒");
}
//return fileByte;
//MessageBox.Show("转换成功!");
}
catch (Exception ex)
{
//MessageBox.Show("转换失败:" + ex.Message);
}
}
/// <summary>
/// 创建导出DataTable
/// </summary>
/// <param name="_curveNameStr"></param>
/// <returns></returns>
private DataTable CreateDt(string[] _curveNameStr)
{
DataTable _dt = new DataTable();
_dt.Columns.Add("#DEPTH", typeof(float));
foreach (string str in _curveNameStr)
{
_dt.Columns.Add(str, typeof(string));
}
return _dt;
}
/// <summary>
/// 写Txt文件
/// </summary>
/// <param name="dirTXT">保存目录</param>
/// <param name="curveNameStr">曲线串</param>
/// <param name="sTDEP">起始深度</param>
/// <param name="eNDEP">终止深度</param>
/// <param name="rLEV">维的采集或计算增量</param>
/// <param name="dt">输出数据</param>
private void WriteTxt(string dirTXT, string curveNameStr, string sTDEP, string eNDEP, string rLEV, DataTable dt)
{
string writeStr = string.Empty; //写入数据
string nullValue = "-9999.0000"; //空值默认
string val = string.Empty; //写入值
int pos = 12; //设置文本间距
using (FileStream fs = new FileStream(dirTXT, FileMode.Create))
{
StreamWriter sw = new StreamWriter(fs);
sw.Write("STDEP = " + sTDEP + "" + "\r\n");
sw.Write("ENDEP = " + eNDEP + "" + "\r\n");
sw.Write("RLEV = " + rLEV + "" + "\r\n");
sw.Write("CURVENAME = " + curveNameStr + "" + "\r\n");
sw.Write("END" + "\r\n");
foreach (DataColumn col in dt.Columns)
{
col.ColumnName = col.ColumnName.Length < pos ? col.ColumnName.PadRight(pos, ' ') : col.ColumnName;
writeStr += col.ColumnName;
}
writeStr = writeStr.Substring(0, writeStr.LastIndexOf(" "));
sw.Write(writeStr + "\r\n"); //写列名
//开始写入曲线数据
for (int i = 0; i < dt.Rows.Count; i++)
{
writeStr = string.Empty; //每行写入数据
foreach (DataColumn col in dt.Columns)
{
val = string.IsNullOrEmpty(dt.Rows[i][col].ToString()) ? nullValue : dt.Rows[i][col].ToString();
val = val.Length < pos ? val.PadRight(pos, ' ') : val;
writeStr += val;
}
writeStr = writeStr.TrimEnd(); //去除尾部空格
sw.Write(writeStr + "\r\n");
}
//清空缓冲区
sw.Flush();
//关闭流
sw.Close();
fs.Close();
}
}
}
原始写法用的是DataTable的,我耐心看了很久(主要是中间一个if判断的end逻辑,我真琢磨了半天),好消息是最后大概能看懂逻辑。
大概逻辑就是从 StartDepth 到 EndDepth,以 StepDepth 为间隔,查找在指定的曲线中depth最为接近的点,并输出其对应的数据。
在几条曲线算完后,通过 WriteFile 写入到文件中。
具体代码逻辑这里不再分析了,有兴趣的可以看看。
然后上面的代码我跑了一下基准。
嗯……雀食有点慢,亿点点慢。

……花了153秒多一点,差不多两分半。
那么那李慢呢。
#4. 干掉LINQ
如果你仔细看过上面的代码的话,会发现,下面这条语句确实是万恶之源。
depth = Depths.Aggregate((current, next) => Math.Abs((long)current - o) < Math.Abs((long)next - o) ? current : next);
写法很溜,但这句话确实是时间复杂度为 O(mn) 的写法。
在题设条件下,这句话大概会产生26.5亿次比较、53亿次计算差值及取绝对值。
这里用了LINQ的写法,一个冷知识,LINQ绝大多数情况下比for之类的朴素循环要慢得多,所以可以先干掉LINQ看看。
// depth = Depths.Aggregate((current, next) => Math.Abs((long)current - o) < Math.Abs((long)next - o) ? current : next); depth = float.MaxValue; foreach (var d in Depths) { if (Math.Abs((long)d - o) < Math.Abs((long)depth - o)) { depth = d; } }
一顿操作猛如虎,一看时间短了……
数据计算完成,耗时 136417毫秒
数据写入完成,耗时 85毫秒
18秒,你就说快没快吧,已经快了10%,向成功迈进了一大步可不是。
#5. 干掉O(mn)
正所谓好钢要用在刀把上。
我们仔细看看上面的代码,会觉得那个 O(m) 的算法实在太过于猖狂了。
那么我们有办法让他变成 O(m) 的算法吗。
那自然有。
仔细看看整个计算过程,我们会发现,要查找数据的Depth序列其实是一条单调递增的序列。
那么,如果我们要查找的目标数据也是一条单调递增的序列,这两条同样单调递增的序列是不是就可以成为两个并排的序列,取两个游标直接比就可以了?
在看完算法后,这完全是可行的。
于是在这个思路基础之上,我们搞出了一个计算器2.0。
public override void Calculate()
{
var start = StartDepth.ToSingle();
var end = EndDepth.ToSingle();
var step = StepDepth.ToSingle();
var curveName = CurveNames;
var wm = WisModel;
var st = new Stopwatch();
st.Start();
// 目标数组
var data = new List<float[]>();
// 创建目标数据序列
for (var temp = start; temp <= end; temp += step)
{
var item = new float[curveName.Length * (Verbose ? 3 : 1) + 1]; // add depth & diff data
item[0] = temp;
data.Add(item);
}
// 计算数组
for (var i = 0; i < curveName.Length; i++)
{
var channel = FindChannel(wm, curveName[i]);
if (channel == null)
continue;
var arrIndex = i + 1; //2- add depth
// 预处理数据
var depths = channel.Depths.Select((d, x) => new { d, v = channel.Values[x] }).OrderBy(s => s.d).ToArray();
// 对每个数据进行检索
var index = 0;
var vIndex = 0;
foreach (var item in data)
{
var depth = item[0];
// 搜索差值最小的点
var diff = float.MaxValue;
for (; index < depths.Length; index++)
{
var diff1 = Math.Abs(depths[index].d - depth);
if (diff1 < diff)
{
diff = diff1;
vIndex = index;
item[arrIndex] = depths[index].v;
}
else
{
// 如果已经开始背离了,则说明已经找到最小点,应停止
// 回退一个,避免下一个最接近点也是当前点的情况
index--;
break;
}
}
item[arrIndex] = diff > 10.000f ? -9999f : depths[vIndex].v;
}
}
Console.WriteLine($"数据计算完成,耗时 {st.ElapsedMilliseconds}毫秒");
st.Restart();
//写入文件
WriteFile(curveName, start, end, step, TargetFile, data);
st.Stop();
Console.WriteLine($"数据写入完成,耗时 {st.ElapsedMilliseconds}毫秒");
}
public void WriteFile(string[] curveName, float start, float end, float step, string targetFile, List<float[]> data)
{
var sw = new StreamWriter(targetFile, false, Encoding.UTF8);
void WriteString(string str, bool padding = true)
{
sw.Write(str);
if (padding) sw.Write(_paddingStrMap.GetValue(12 - str.Length, len => "".PadRight(len, ' ')));
}
// TODO: 测试的时候发现很奇怪的事儿,.net 4.x 下如此输出的浮点数只有三位小数
void WriteValue(float value, bool padding = true) => WriteString(Math.Round(value, 6).ToString("F6"), padding);
sw.Write("STDEP = " + start.ToString("F4") + "\r\n");
sw.Write("ENDEP = " + end.ToString("F4") + "\r\n");
sw.Write("RLEV = " + step.ToString("F4") + "\r\n");
sw.Write("CURVENAME = " + curveName.JoinAsString(", ") + "\r\n");
sw.Write("END" + "\r\n");
// 写入表头
WriteString("#DEPTH");
for (var i = 0; i < curveName.Length; i++)
{
WriteString(curveName[i], i < curveName.Length - 1);
}
sw.WriteLine();
// 写入数据
foreach (var item in data)
{
for (var i = 0; i < item.Length; i++)
{
WriteValue(item[i], i < item.Length - 1);
}
sw.WriteLine();
}
}
这里关键的一步,就是预处理。这步的操作目标,是将曲线中的深度与数值配对后,进行排序。生成新的数组后,和当前的深度序列使用两个游标进行比较,类似于快慢指针。那么,每个曲线,理论上只需要比较一次就行,以当前的数据集为例,大概是5W次多一点。
那么这个新的算法大概需要多久呢?

20毫秒,比文件写入还快。
#6. 快有啥用,还要准
我们都知道,快其实是次要的,准才是最重要的。
我在搞完上面这个算法后,第一时间做的事情,是比较生成的数据(和原始版本生成的数据)进行对比,会发现:数据差异也忒大了。
搞到这里的时候抑郁了半天。
仔细核对了一遍又一遍,没感觉这代码有明显哪里的问题啊,怎么会数据差这么大,你说离谱吧,还都有数据。
很奇怪。
思考了很久后,我觉得,如果发现自己的问题实在摆不平了,那就不要内耗,不要自我反思,要勇于指责他人。
于是我回过头去看上面的原始代码。
如果你有非常仔细的看过原始代码的话,那应该……也许应该吧……
depth = Depths.Aggregate((current, next) => Math.Abs((long)current - o) < Math.Abs((long)next - o) ? current : next);
不觉得奇怪吗,为什么比较差值的时候要先转为long?带着这个疑问,我去问了原作者……
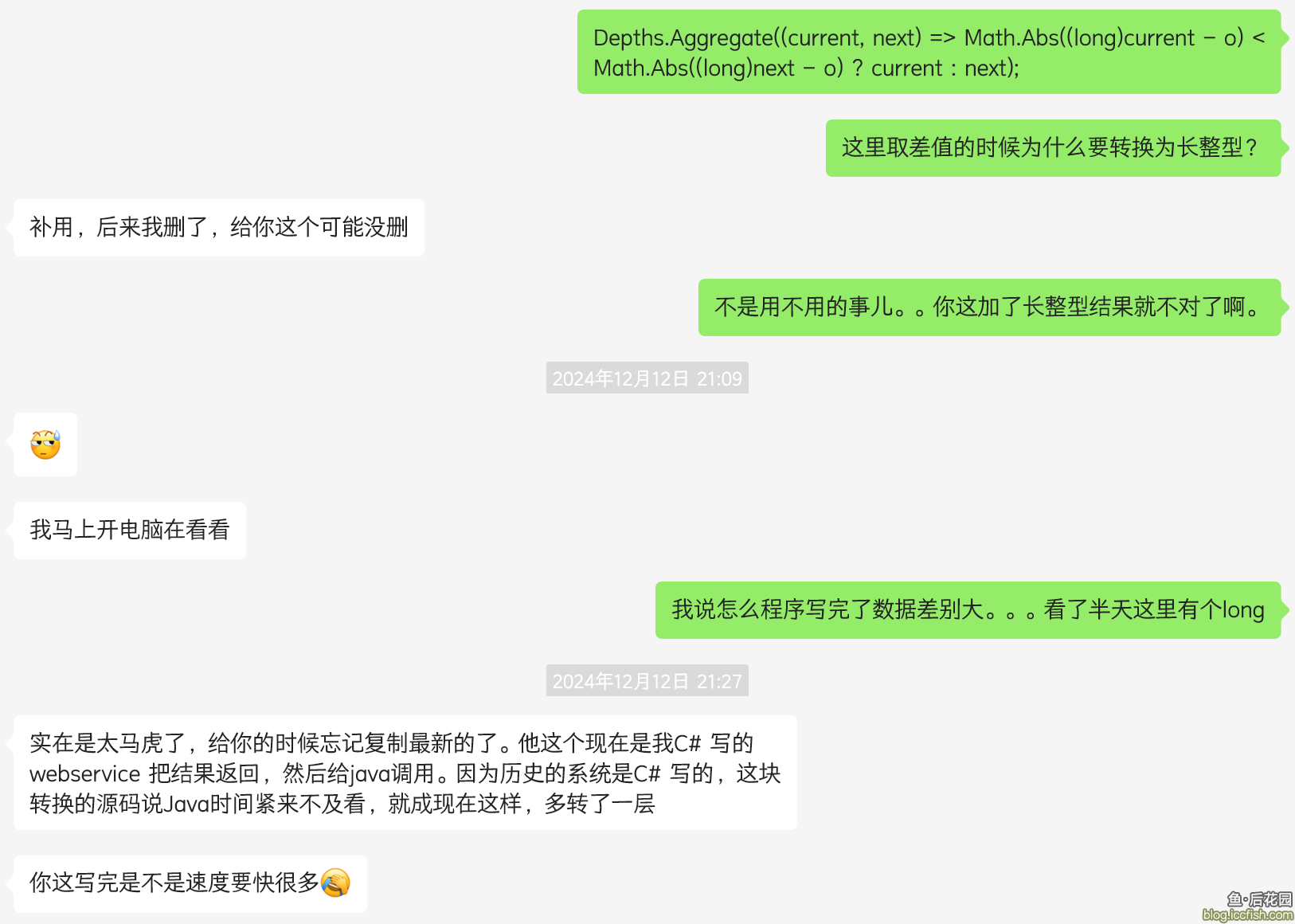
……行的吧。
然后他找了几份原系统里导出来的数据供我参考。
这不参考还好,一参考头皮麻,数据有很多对不上号的。
这到底咋回事呢。
这时候我才仔细看了看原始数据,发现原始数据的采样深度都是单调递增的。如果所有的数据都是这样,那之前代码里的排序逻辑也许可以省略,但因为我对这方面的事情不太了解,所以还是不要做此假定为好。
#7. 间隔能不能看着精准点?
天天用浮点数去比较的人都知道,浮点数这玩意儿,搁计算机里,就不太可能精准。
于是对比的时候有个事儿就很让我膈应。
不止上面写出来的程序,包括他提供的参考数据,都有这个问题。
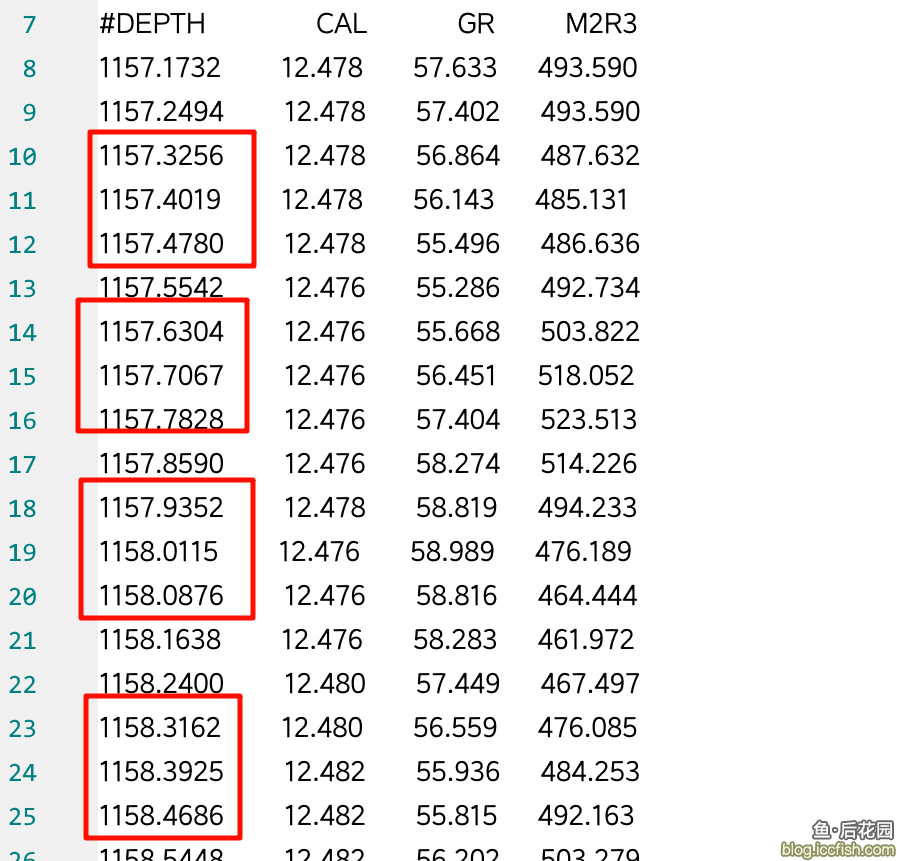
我们给出的间隔是 0.0762,那么理论上来说我们期望看到的是完美的序列。
但是这样的数据下,总有个别位表现为跳动。
有办法解决这个问题吗?应该……有吧?
询问了下数据处理精度,基本上都要求四位小数。
那么要规避这个问题最简单的方式,那就是:不要用浮点数。
public override void Calculate()
{
var start = (long)Math.Round(StartDepth.ToDouble() * 10000);
var end = (long)Math.Round(EndDepth.ToDouble() * 10000);
var step = (long)Math.Round(StepDepth.ToDouble() * 10000);
var curveName = CurveNames;
var wm = WisModel;
var st = new Stopwatch();
st.Start();
// 目标数组
var data = new List<long[]>();
// 创建目标数据序列
for (var temp = start; temp <= end; temp += step)
{
var item = new long[curveName.Length * (Verbose ? 3 : 1) + 1]; // add depth & diff data
item[0] = temp;
data.Add(item);
}
// 计算数组
for (var i = 0; i < curveName.Length; i++)
{
var channel = FindChannel(wm, curveName[i]);
if (channel == null)
continue;
var arrIndex = i + 1; //2- add depth
// 预处理数据
var depths = channel.Depths.Select((d, x) => new { d = (long)Math.Round(d * 10000), v = (long)Math.Round(channel.Values[x] * 10000) }).OrderBy(s => s.d).ToArray();
// 对每个数据进行检索
var index = 0;
var vIndex = 0;
foreach (var item in data)
{
var depth = item[0];
// 搜索差值最小的点
var diff = long.MaxValue;
for (; index < depths.Length; index++)
{
var diff1 = Math.Abs(depths[index].d - depth);
if (diff1 < diff)
{
diff = diff1;
vIndex = index;
item[arrIndex] = depths[index].v;
}
else
{
// 如果已经开始背离了,则说明已经找到最小点,应停止
// 回退一个,避免下一个最接近点也是当前点的情况
index--;
break;
}
}
item[arrIndex] = diff > 10 * 10000 ? -9999 * 10000L : depths[vIndex].v;
}
}
Console.WriteLine($"数据计算完成,耗时 {st.ElapsedMilliseconds}毫秒");
st.Restart();
//写入文件
WriteFile(curveName, start, end, step, TargetFile, data);
st.Stop();
Console.WriteLine($"数据写入完成,耗时 {st.ElapsedMilliseconds}毫秒");
}
public void WriteFile(string[] curveName, long start, long end, long step, string targetFile, List<long[]> data)
{
var sw = new StreamWriter(targetFile, false, Encoding.UTF8);
void WriteString(string str, bool padding = true)
{
sw.Write(str);
if (padding) sw.Write(_paddingStrMap.GetValue(12 - str.Length, len => "".PadRight(len, ' ')));
}
void WriteValue(long value, bool padding = true) => WriteString((value / 10000.0).ToString("f4"), padding);
sw.WriteLine("FORWARD_TEXT_FORMAT_1.0");
sw.Write("STDEP = ");
WriteValue(start, false);
sw.Write("\r\nENDEP = ");
WriteValue(end, false);
sw.Write("\r\nRLEV = ");
WriteValue(step, false);
sw.Write("\r\nCURVENAME = " + curveName.JoinAsString(", ") + "\r\n");
sw.Write("END" + "\r\n");
// 写入表头
WriteString("#DEPTH");
for (var i = 0; i < curveName.Length; i++)
{
WriteString(curveName[i], i < curveName.Length - 1);
}
sw.WriteLine();
// 写入数据
foreach (var item in data)
{
for (var i = 0; i < item.Length; i++)
{
WriteValue(item[i], i < item.Length - 1);
}
sw.WriteLine();
}
sw.Close();
}
最简单的思路。我们都用整形来处理,那么就不会有精度问题了。输出的时候运算回去即可。
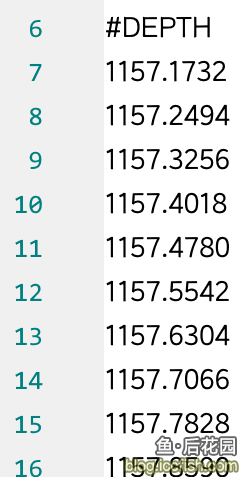
……终于治好了我该死的强迫症。
其实如果精度还可以再高点,多留小数位。有兴趣的可以试试。
#8. 搞搞并行?
再次观察一下,我们会发现,要输出的曲线和曲线之间,其实是不冲突的。那摸问题来了,可否改成并行?
但是看了看执行时间,感觉平均每条曲线10毫秒不到,才三条曲线,改成并行的意义似乎不是很大。
但我还是测了测。
public override void Calculate()
{
var start = (long)Math.Round(StartDepth.ToDouble() * 10000);
var end = (long)Math.Round(EndDepth.ToDouble() * 10000);
var step = (long)Math.Round(StepDepth.ToDouble() * 10000);
var curveName = CurveNames;
var wm = WisModel;
var st = new Stopwatch();
st.Start();
// 目标数组
var data = new List<long[]>();
// 创建目标数据序列
for (var temp = start; temp <= end; temp += step)
{
var item = new long[curveName.Length * (Verbose ? 3 : 1) + 1]; // add depth & diff data
item[0] = temp;
data.Add(item);
}
// 计算数组
Parallel.For(
0,
curveName.Length,
i =>
{
var channel = FindChannel(wm, curveName[i]);
if (channel == null)
return;
var arrIndex = i + 1; //2- add depth
// 预处理数据
var depths = channel.Depths.Select((d, x) => new { d = (long)Math.Round(d * 10000), v = (long)Math.Round(channel.Values[x] * 10000) }).OrderBy(s => s.d).ToArray();
// 对每个数据进行检索
var index = 0;
var vIndex = 0;
foreach (var item in data)
{
var depth = item[0];
// 搜索差值最小的点
var diff = long.MaxValue;
for (; index < depths.Length; index++)
{
var diff1 = Math.Abs(depths[index].d - depth);
if (diff1 < diff)
{
diff = diff1;
vIndex = index;
item[arrIndex] = depths[index].v;
}
else
{
// 如果已经开始背离了,则说明已经找到最小点,应停止
// 回退一个,避免下一个最接近点也是当前点的情况
index--;
break;
}
}
item[arrIndex] = diff > 10 * 10000 ? -9999 * 10000L : depths[vIndex].v;
}
});
//Console.WriteLine(data.Take(10).Select(s => s.Select(x => ((x / 10000.0).ToString("f4"))).JoinAsString("\t")).JoinAsString("\n"));
Console.WriteLine($"数据计算完成,耗时 {st.ElapsedMilliseconds}毫秒");
st.Restart();
//写入文件
WriteFile(curveName, start, end, step, TargetFile, data);
st.Stop();
Console.WriteLine($"数据写入完成,耗时 {st.ElapsedMilliseconds}毫秒");
}
计算耗时17毫秒,确实下降了些(30%),但是因为基数本来就比较低,因此不太明显。如果数据量更大,或者曲线更多的时候,似乎更有优势一点,这里表现不太明显。
#9. 怎么还有差异?
现在的问题是,和大兄弟提供的参考结果数据,总有些差异,非常费解,可能这也是花了我比较多时间的关系,关键是这个中差异大兄弟也无法解释,因为不了解旧系统的逻辑。
这里的差异主要包括以下几个。
9.1 无效数据
根据数据逆向推测,在数据文件中的-9999应该属于无效数据。但是对于-9999无效数据的处理方式,却在结果数据中表现出不一致性,就比较让人费解。比如在开始处的-9999,在结果文件中就被忽略了,表现是结果中的对应深度数值是下一个有效点。
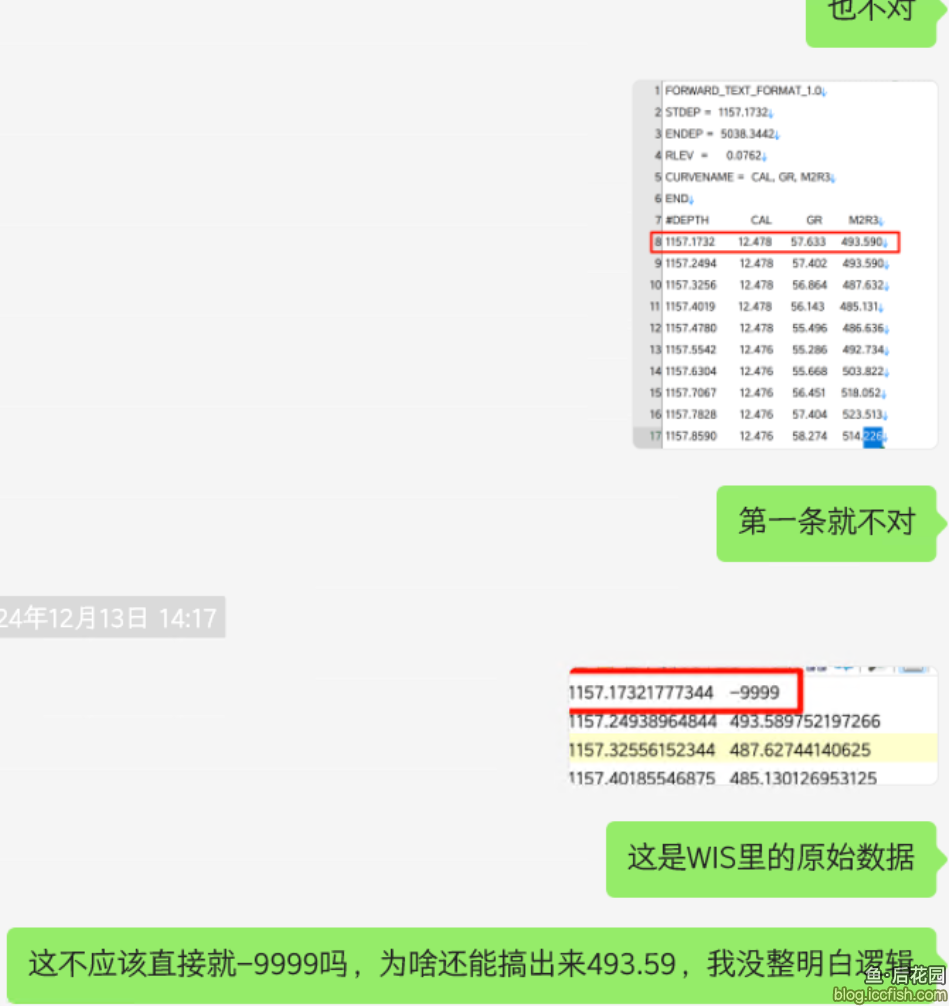
但与此同时,最后面的数据时,这些-9999的原始数据好像又被当做有效数据处理了,这种歧义就非常让人费解。
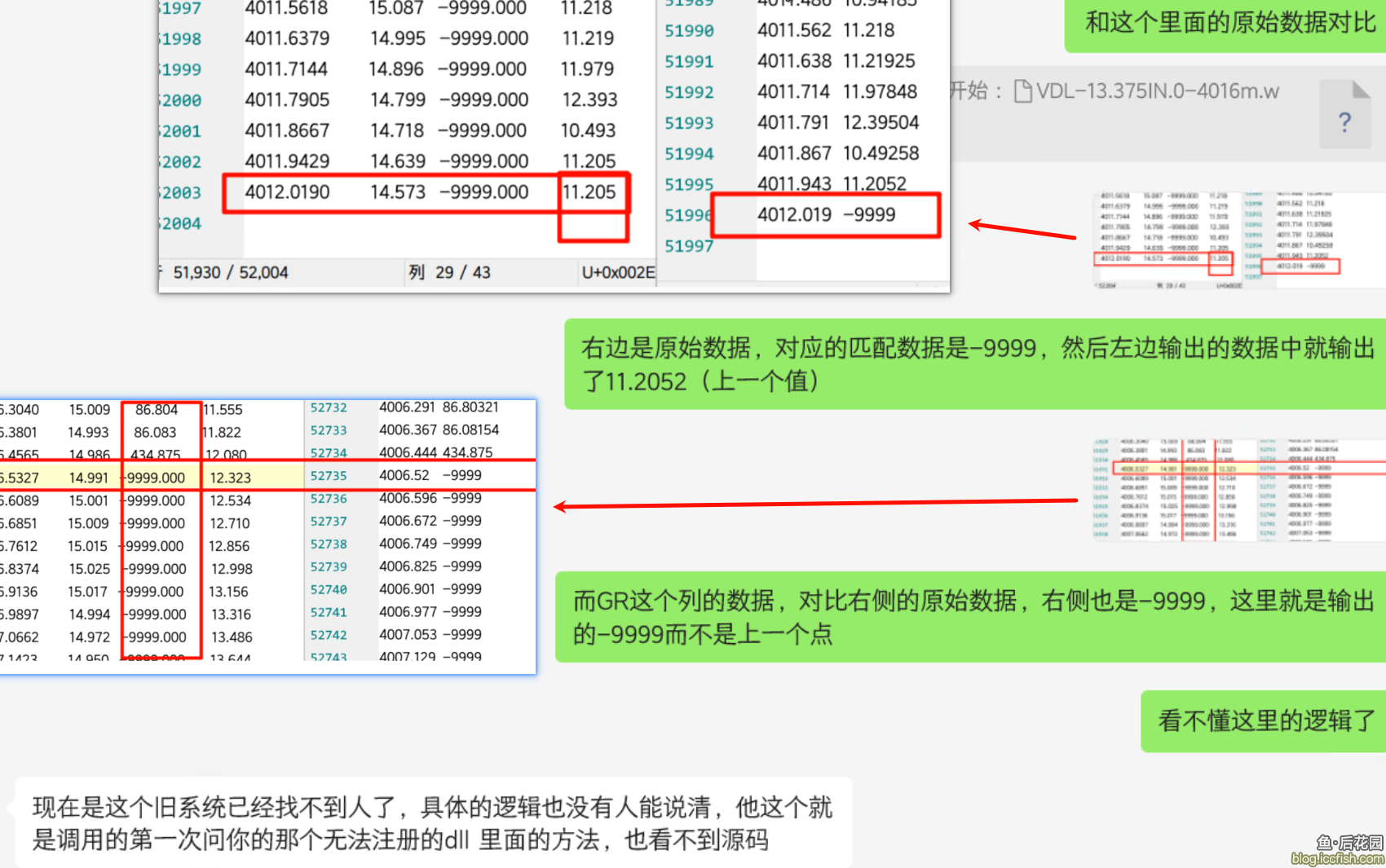
由于大兄弟也说不清楚这里的逻辑,那我姑且认为过滤掉-9999这样无意义的原始数据会更符合语义一点。过滤方式倒也是特别简单。
// 预处理数据 var depths = channel.Depths.Select((d, x) => new { d = (long)Math.Round(d * 10000), v = (long)Math.Round(channel.Values[x] * 10000) }) .Where(s => s.v > -99000000) .OrderBy(s => s.d) .ToArray();
9.2 与别的软件的差异性
由于无法得知旧系统的数据处理逻辑,因此大兄弟找来了三方软件数据进行参考。
这下更麻烦了,有大部分数据一致,但小部分数据不一致但差别很小。大兄弟觉得这可能是因为软件进行了插值导致的。
但是插值的话,第一行数据咋个插法,没整明白。

另一个问题是,这个三方软件不同的功能位置导出的原始数据会有点差异,具体差异位置,大兄弟猜测可能是插值导致的。
至此,由于实在是专业性限制了我,加上大兄弟原始需求就是找到最接近的点,那边就此作罢。
#10. 要不顺便插个值?
倒也是简单。
public override void Calculate()
{
var start = (long)Math.Round(StartDepth.ToDouble() * 10000);
var end = (long)Math.Round(EndDepth.ToDouble() * 10000);
var step = (long)Math.Round(StepDepth.ToDouble() * 10000);
var curveName = CurveNames;
var wm = WisModel;
var st = new Stopwatch();
st.Start();
// 目标数组
var data = new List<long[]>();
// 创建目标数据序列
for (var temp = start; temp <= end; temp += step)
{
var item = new long[curveName.Length * (Verbose ? 3 : 1) + 1]; // add depth & diff data
item[0] = temp;
data.Add(item);
}
// 计算数组
for (var i = 0; i < curveName.Length; i++)
{
var channel = FindChannel(wm, curveName[i]);
if (channel == null)
continue;
var arrIndex = i + 1; //2- add depth
// 预处理数据
var depths = channel.Depths.Select((d, x) => new { d = (long)Math.Round(d * 10000), v = (long)Math.Round(channel.Values[x] * 10000) })
.Where(s => s.v > -99000000)
.OrderBy(s => s.d)
.ToArray();
// 对每个数据进行检索
var index = 0;
var vIndex = 0;
foreach (var item in data)
{
var depth = item[0];
// 搜索差值最小的点
var diff = long.MaxValue;
for (; index < depths.Length; index++)
{
var diff1 = Math.Abs(depths[index].d - depth);
if (diff1 < diff)
{
diff = diff1;
vIndex = index;
}
else
{
// 如果已经开始背离了,则说明已经找到最小点,应停止
// 回退一个,避免下一个最接近点也是当前点的情况
index--;
break;
}
}
if (diff > 10 * 10000)
{
item[arrIndex] = -9999 * 10000L;
}
else
{
if (vIndex == 0 || vIndex == depths.Length - 1 || depths[vIndex].d == depth)
item[arrIndex] = depths[vIndex].v;
else if (depths[vIndex].d < depth)
{
// 当前点在采样点右侧,向上插值
item[arrIndex] = (long)Math.Round((depth - depths[vIndex].d) * (depths[vIndex + 1].v - depths[vIndex].v) * 1.0 / (depths[vIndex + 1].d - depths[vIndex].d) + depths[vIndex].v);
}
else
{
// 当前点在采样点左侧,向下插值
item[arrIndex] = (long)Math.Round((depth - depths[vIndex - 1].d) * (depths[vIndex].v - depths[vIndex - 1].v) * 1.0 / (depths[vIndex].d - depths[vIndex - 1].d) + depths[vIndex - 1].v);
}
}
}
}
//Console.WriteLine(data.Take(10).Select(s => s.Select(x => ((x / 10000.0).ToString("f4"))).JoinAsString("\t")).JoinAsString("\n"));
Console.WriteLine($"数据计算完成,耗时 {st.ElapsedMilliseconds}毫秒");
st.Restart();
//写入文件
WriteFile(curveName, start, end, step, TargetFile, data);
st.Stop();
Console.WriteLine($"数据写入完成,耗时 {st.ElapsedMilliseconds}毫秒");
}
插值后效率有所降低,上述代码实际测试单次耗时37毫秒。
这里其实有问题,这里假定测量数据是连续的且不会有交叉重复的,否则插值无意义,所以这里仅用于……无聊吧。。
#11. 还有更多的吗?
到这里暂时完结。
必须提醒:
- 前述代码没有完整测试过,可能存在未知错误,谨慎对待,辩证测试
- 性能测试只跑一次,具备较强随机性,仅供参考
说到这里,我突然在想一个问题,如果哈,我是说如果,一个wis中各个曲线的数据对应的深度都是一致的,那么还有办法可以进一步加个速,大概逻辑就是先行比较深度,对不同深度的数据索引计算完毕后,一次性取好即可。
但由于我不确定数据是否确实这样(因为手上只有一两个数据文件也不能代表所有),所以就此按下,有需要的可以研究研究。
哎嗨。
一转眼25号了。
哎嗨嗨嗨。


